我們搬家囉~~~

我們搬家囉~~~

最新文章以及近期活動請到以下新網址點閱

科學X博士 : http://doctorx9000.com

【科展解析】你吃進了多少毒素？免洗筷二氧化硫殘留量測定

【科展解析】你吃進了多少毒素？免洗筷二氧化硫殘留量測定

我們想知道崙背地區小吃店、餐廳、便利商店、夜市所提供的免洗筷是否含有二氧 化硫殘餘？殘餘量高不高？

【X博士摘要說明】

1.  利用精密裝置來檢測十種樣本含有二氧化硫的情形。

2.  希望提供消費者在使用免洗筷時，利用簡易泡水法來減少二氧化硫殘餘。

3.  希望提供消費者在購買家用筷子後，利用液體的酸鹼特性來去除二氧化硫殘餘。

第 46 屆國小自然科作品

題目：你吃進了多少毒素？免洗筷二氧化硫殘留量測定

作者：雲林縣崙背鄉崙背國民小學的同學們

【摘要(原文)】

最近網路和新聞媒體都頻頻出現免洗筷有毒的新聞，引起大眾的一陣恐慌，平日經常使用免洗筷的我很注意這個議題,趁著這次科展便邀了班上幾個志同道合的朋友，一起來為我們生活周遭的免洗筷做個總體檢，看看我們平常所使用的免洗筷是否安全衛生，有無殘留二氧化硫。在實驗中發現我們生活周遭所使用的免洗筷二氧化硫含量均不高，而且可以利用水洗的方式去除。每一種廠牌的免洗筷不論是外包裝或是筷子本身都有明顯的差異，在實驗過程中我們發現無標示公司或製造日期，筷身染墨有黑線條、聞起來酸味重的免洗筷其二氧化硫含量較高。所以消費者在使用免洗筷時可以特別的注意外觀、聞起來的氣味，最好可以用熱水洗一下，以去除附著在免洗筷上的二氧化硫。

【X博士步驟說明】

●精密裝置檢測二氧化硫殘留量

原理：亞硫酸鹽在酸性條件下加熱，蒸出二氧化硫，然後以雙氧水溶液吸收並氧 化成硫酸，在以標準鹼液滴定之。

實驗中抽查免洗筷 10 件，不含二氧化硫產品為 4 件，含二氧化硫免洗筷為 6 件，佔 60﹪，二氧化硫量值均低為 228.8ppm 以下，免洗筷中仍含有少量二氧化硫，為維護人體健康建議減少免洗筷使用量，或者使用免洗筷包裝上已有標示不含「漂白劑」的產品。

●去除二氧化硫的方法

1.二氧化硫在米酒中溶出較多，而且煮越久可能是因為酒精揮
發的關係，二氧化硫濃度越來越小。

2.建議吃燒酒雞及薑母鴨時，不要使用免洗筷。

3.建議喝汽水時，不應用免洗筷攪拌。

建議使用在使用免洗筷之前，可先以清水清洗十五分鐘後在使用。 

數據分析與結論

有清洗後的免洗筷，二氧化硫的溶出量和清洗前的免洗筷作對比， 有大幅的降低。建議喝汽水時，不應用免洗筷攪拌。而二氧化硫在米酒的溶出量卻出乎意料的高，所以可以建議新購家用竹筷時，不妨利用米酒清洗來降低二氧化 硫的含量。

以下是評審給的評語

【X博士評語】

廠商為求免洗筷的美觀，都會做「漂白」的程序，而其中又以二氧化硫最為普遍，為了照顧我們的健康，外食可以自備環保筷，並讓我們共同響應「一人一筷健康愉快」及「愛護地球拒用免洗筷」吧。長此以往，我們不但擁有健康的身體，更保護地球的生態環境。

【科展解析】科學玩具 DIY─神秘地雷包

【科展解析】科學玩具 DIY─神秘地雷包

   

有一天下課，一群同學圍在走廊上尖叫，只見其中的一名同學拿著一包用鋁箔袋包裝的 小東西，用腳輕輕的往袋子一踩，袋子便漸漸脹大。不一會，「砰！」一聲，響徹整個走廊。大家議論紛紛，小小的袋子為什麼會爆炸呢？


【X博士摘要說明】

1. 想了解地雷包為什麼會爆炸？


2. 想自己動手做地雷包。

第 45 屆 國小自然科作品

題目：科學玩具 DIY─神秘地雷包

作者：臺北縣板橋市溪洲國民小學的同學們


【摘要(原文)】

我們無意中發現有人在玩『地雷包』，由於好奇，想了解地雷包為什麼會爆炸？也想自己動手做地雷包，於是將心中的一連串問題，參考自然課本「酸與鹼」和「氧氣與二氧化碳」二個單元，與同學著手設計實驗，最後我們發現原來地雷包是利用「酸鹼中和原理」產生二氧化碳將其外包裝撐破而達到爆破效果，並發現利用適量的小蘇打粉加上 30%~40%檸檬酸或40%~60%的醋酸，便可輕輕鬆鬆 DIY「神秘地雷包」。

【X博士步驟說明】

●檢測地雷包內的氣體成份。
1、將市售地雷包中所有的成份直接放入廣口瓶中反應，置入點燃的線香。
2、將市售地雷包產生的氣體引入澄清石灰水中，觀察其變化。

   


●利用石蕊試紙及廣用試紙檢測地雷包內容物的酸鹼性。

1、將地雷包內白色粉末調配成5%的水溶液，利用石蕊試紙及廣用試紙測pH值。
2、直接取市售地雷包透明溶液，利用石蕊試紙及廣用試紙測 pH 值。
   

1、市售地雷包內的白色粉末使紅色及藍色石蕊試紙均呈藍色；以廣用試紙檢測， pH 為 9.0 左右，所以此白色粉末為一鹼性粉末。
2、市售地雷包內的溶劑使紅色及藍色石蕊試紙均呈紅色；以廣用試紙檢測， pH 為 2.0左右，所以此溶液為一酸性溶液。


●檢測地雷包爆炸後產物的酸鹼性。

1、利用廣用試紙測爆炸後袋外液體的酸鹼性。
2、利用廣用試紙測爆炸後袋內液體的酸鹼性。
   
1、市售地雷包爆炸後，袋外的液體，呈中性反應；袋內液體呈鹼性反應。推測地雷包是利用酸鹼中和原理。
2、爆炸後的市售地雷包內發現有些許的鹼性粉末殘留，過量的鹼性粉末有助於將所有的強酸溶液中和，其目的為增加地雷包遊戲時的安全性。


●如何自製地雷包？
1、酸性液體：酸性液體為 40%檸檬酸、30%檸檬酸、 40%醋酸、60%醋酸。
2、鹼性粉末：試藥級小蘇打粉及食用級小蘇打粉
3、從步驟 1 選用一種酸性溶液取約 5~9 毫升，裝入最小號的夾鍊袋中，並用封口機封住袋口，製成一袋酸性溶液。
4、將回收的零食鋁箔紙袋，裁成與市售品一致的大小(8.5 公分×10.5 公分)，當地雷包的外包裝。選用步驟 2 的鹼性粉末 4 克置入袋內。
5、將步驟 3 的酸性溶液，置入步驟 4 裝有小蘇打粉的回收的零食鋁箔袋中，利用封口機封緊袋口，即輕輕鬆鬆完成『神秘地雷包』。
   

數據分析與結論

原來市售地雷包的爆炸原理是利用酸和碳酸鹽混合後，進行酸鹼中和反應產生二氧化碳，撐破塑膠袋時所發生的劇響。從日常生活常見的酸中發現，40%檸檬酸是最適合用於做自製地雷包的酸性溶液，主要是檸檬酸溶於水中無特殊的刺鼻酸味，及在相同的條件下其產生的二氧化碳的氣體比其 他酸性溶液多，甚至高於市售地雷包；而 40%醋酸、60%醋酸及 30%檸檬酸其產生二氧化碳的量也高於市售地雷包，可供作自製地雷包不同的選擇。


以下是評審給的評語
   


【X博士評語】

利用回收後的零食外包裝製作地雷包，其外觀多樣精美，不亞於市售地雷包。讓隨手丟棄的小垃圾，增添了不少新的生活樂趣，甚至可以在外包裝上多加巧思，不仿可以試試看。

【科展解析】從高鐵紀念車票注入感熱紙新生命

 

正當全台灣大眾歡欣鼓舞慶賀高鐵通車帶來南來北往不可思議的便利時，卻對感熱紙製成的車票發出怒吼，唯恐經過一段時日後這張紀念票成了無字天書。這倒引起我的好奇心，生活中隨處可見的感熱紙，究竟是什麼奇妙的紙張，字跡會自行消失又不能護貝保存呢﹖

 

【X博士摘要說明】

1. 設計實驗分析感熱紙的特性


2. 測試感熱紙文字圖像出現的原因


3. 找出可能影響感熱紙文字圖像消失的因素


4. 發掘感熱紙的新用法

 

第 47 屆 國小生活與應用科學科科作品

題目：從高鐵紀念車票注入感熱紙新生命

作者：臺北市中山區長安國民小學的同學們

 

【摘要(原文)】

由高鐵紀念車票的新聞，讓我們徹底研究感熱紙的特性:從紙上文字的出現到消失的各種因素。我們發現感熱紙真的可以製成紙色均勻的再生紙，並不會污染環境。最重要的是文字消失後的感熱紙可以再次使用。別以為文字消失就很安全，它可是無字天書呢！大家也不必再擔心便利商店的繳費收據變為白紙後，會發生認證上的困難，家庭必備的電熨斗可以讓證據再現！

 

【X博士步驟說明】

●感熱紙上文字圖像的浮現

感熱紙出現黑色文字圖像的條件: 須要接觸到 70°C 以上的高溫。

   

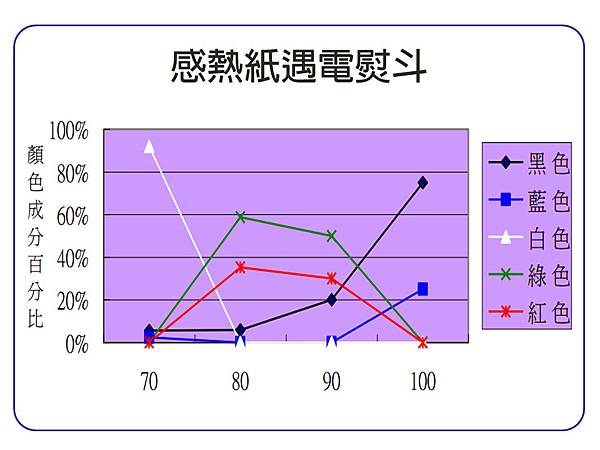
感熱紙出現黑色文字圖像的條件: 強酸(Ph1)

   

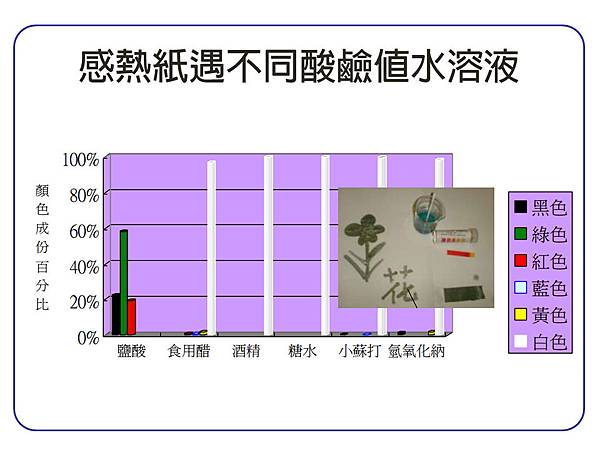
感熱紙出現黑色文字圖像的條件: 壓力

   

 

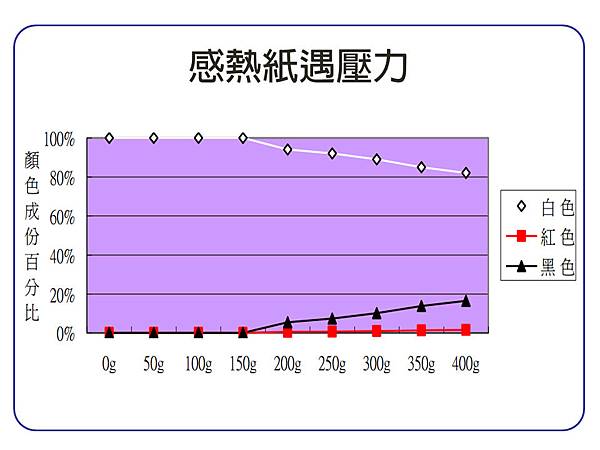
●感熱紙的新生命

1. 感熱紙製成之再生紙滴入鹽酸後，仍舊呈現藍黑色。

2. 感熱紙紙漿呈中性。

3. 酒精浸泡再生紙後，滴入鹽酸，酒精顏色由無色轉為深藍綠色。

   

白色感熱紙加熱變為黑色，上面會有淺灰色的原來印出的資料出現。

   

 

數據分析與結論

1. 經由此實驗我們了解感熱紙的特性為: (一) 遇強酸、熱會變色(二) 酒精會溶解感熱紙的化學塗料。


2. 長期保存感熱紙並不難，只要能將紙存放於真空密封罐(袋)存放於陰暗處，避免高溫陽光，將可長期保存。


3. 廢棄的感熱紙可以製成再生紙，紙色均勻並沒有黑點產生，而原先光滑不利原子筆 書寫的表面也變為粗糙適合書寫。


4. 再生紙製作過程中的廢水呈中性，應不至於對環境造成污染，所以我們認為感熱紙應可回收製成再生紙。


5. 即使感熱紙上文字經自然消失後，仍可再次如新的感熱紙般使用，紙上的化學物質並未消失。


6. 偶然發現的無字天書要提醒大家:感熱紙上的文字雖然消失，但是仍可讓它重現，所以雖然不見文字還是要撕毀不要隨手亂扔。


7. 便利商店以感熱紙呈現的繳款收據，再也不必擔心資料消失苦無證據，只要以電熨斗加熱就不會有爭執產生了！

 

以下是評審給的評語

   

 

【X博士評語】

有關感熱紙單據的保存，除了絕對避免碰觸到酒精、漂白水、鹽酸(強酸) 、氫氧化鈉水溶液 (強鹼)外，平日應存放於黑色真空罐(袋)中，以減少光線及濕氣的干擾。所以不要隨便丟棄變白的自動提款機的感熱紙紀錄，他人可以經由加熱讓你的資料完全顯現。

【科展解析】聲鳴遠播~大聲公的終極挑戰！

 

運動會的時候，我們學校舉辦拔河比賽，很多的老師和班親媽媽都用大聲公喊著「1、2、殺」、「1、2、殺」來加油！於是我們就想到為什麼大聲公可以讓聲音變大呢？大聲公為什麼可以讓聲音傳得比較遠呢？

 

【X博士摘要說明】

1. 大聲公的口徑和材質相同時，不同的長度是否會影響大聲公聲音的大小？


2. 大聲公的長短和材質相同時，不同的口徑是否會影響大聲公聲音的大小？


3. 大聲公的長短和口徑相同時，不同的材質是否會影響大聲公聲音的大小？


4. 不同形狀的大聲公，是否會影響大聲公聲音的大小？


5. 大聲公對不同位置的聲音大小是否會有不同？

 

第 47 屆 國小生活與應用科學科作品

題目：聲鳴遠播~大聲公的終極挑戰！

作者：臺北縣板橋市江翠國民小學的同學們

 

【摘要(原文)】

傳聲筒(一般俗稱大聲公)是在生活中常常可以見到的物品，它能使發出的聲音更加宏亮。本研究的目的即想探索、改良大聲公的各種可能性？所以改變了大聲公的長度、口徑大小、材質、形狀及測試不同位置大聲公的聲音效果，也就是想要進行一項大聲公的終極挑戰，現在就請您仔細看看我們的研究喔！

 

【X博士步驟說明】

●大聲公的口徑和材質相同時，不同的長度是否會影響大聲公聲音的大小？

   

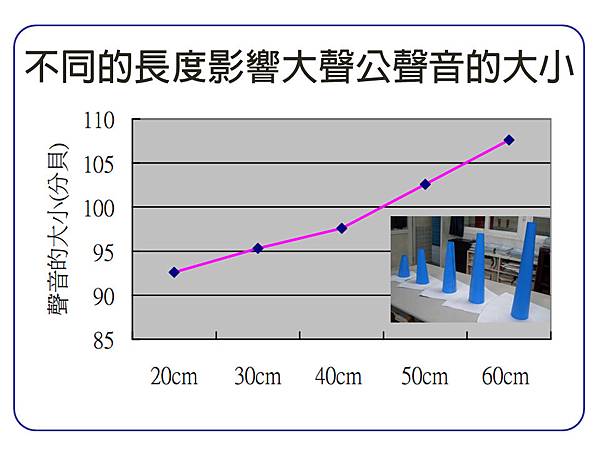
大聲公的長度越長，所得到的聲音越大聲，雖然長度 60 公分的大聲公，必須經過較長的距離，但聲音卻更大，表示聲音經過大聲公管壁內會反射，反而集中更多的能量，聲音沒有散失，所以聲音會更大。

 

●大聲公的長短和材質相同時，不同的口徑是否會影響大聲公聲音的大小？

大聲公的口徑太小或口徑太大，喊出來的聲音，就沒有太大的效果，

   

 

●大聲公的長短和口徑相同時，不同的材質是否會影響大聲公聲音的大小？

   

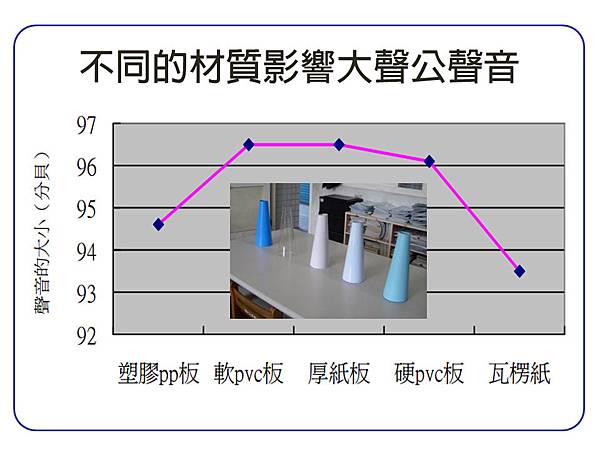
表面平滑或堅硬的物體較容易反射聲音，而集中最大的聲音能量，例如： 軟 pvc 板、厚紙板、硬 pvc 板表面都很光滑，但像塑膠 pp 板的表面不是那麼光滑或有皺摺表面的瓦楞紙就不容易反射聲音。聲音是不是能有效反射，要依所碰到的物體性質來決定。

 

●大聲公的口徑、材質、長短相同，不同形狀的大聲公是否會影響大聲公聲音的大小？

   

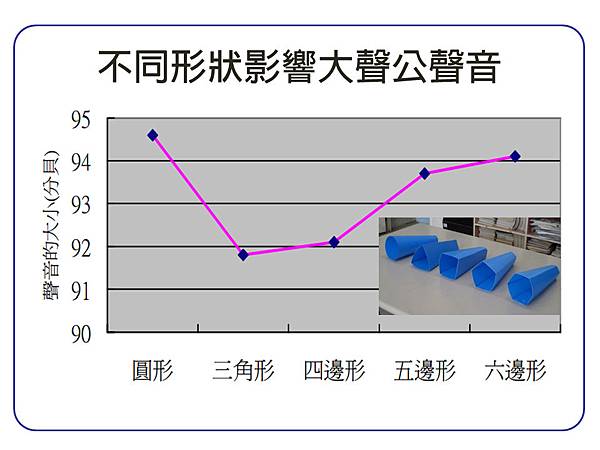
聲音碰到不同形狀的大聲公，會產生不同的集中與反射，所以聲音的大小會有所不同。大聲公的形狀以三角形的效果最差，而以圓形的聲音集中反射效果最好。

 

●大聲公對不同位置的聲音大小是否會有不同？

   

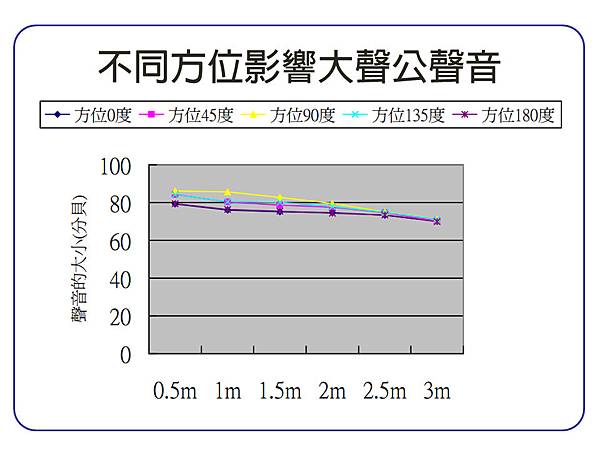
大聲公離分貝計的距離越遠，聲音會遞減。

 

數據分析與結論

若無材料成本的考量，可選擇(1)讓大聲公長度加長；(2) 大聲公前端口徑約在 12 至 22 公分之間；(3)材料以堅硬、光滑易反射聲音的 物質；(4)大聲公的形狀製作成圓形；(5)正面、近距離朝接受聲源者講話，依此方式可得到最佳大聲公的傳聲效果。

 

以下是評審給的評語

   

 

【X博士評語】

簡單的設計不同的變因，就可以研究出讓大聲公提高音量的方法，而其中藉由改良大聲公的方法也極具創意性，而本作品發現，如果要讓大聲公的聲音變大，就必須找讓聲音可以集中的方法，發現以堅硬材質的較長圓形大聲公可以發揮最佳的效果。

【科展解析】數字的鏡子乘法

 

「有一個四位數 ABCD，乘以 4 後得到的答案是 DCBA，請問這個四位數是多少？」。答案為 「2178」─2178×4＝8712。然後我們想到：若這個題目的被乘數為二位到多位，會有什麼樣的答案？如果乘數換成其他正整數，又會有什麼發展？於是我們便著手研究。

 

【X博士摘要說明】

1. 出在十進位制中，符合A1×A2×A3……Am-2×Am-1×Am × N＝Am×Am-1×Am-2……A3×A2×A1的 m位數。


2. 承一，並求出解答之形式及答案數量。


3. 求出十二進位～二進位的鏡子乘法解，並探求其形式及數量。


4. 證明各進位的鏡子乘法解之一般性

 

第 47 屆 國小數學科作品

題目：數字的鏡子乘法

作者：臺北縣三峽鎮三峽國民小學的同學們

 

【摘要(原文)】

我們研究的題目是屬於「覆面算」的一種題型。探討在 n 進位制中，符合

A1×A2×A3……Am-2×Am-1×Am × N＝Am×Am-1×Am-2 ……A3×A2×A1的 m 位被乘數，其中 N＝2～(n－1)，n 為該進位制的「基數」。並歸納在所有進位制中，解答的一般性。

 

【X博士步驟說明】

●探求被乘數 4～13 位的解答(1~3無解)

   

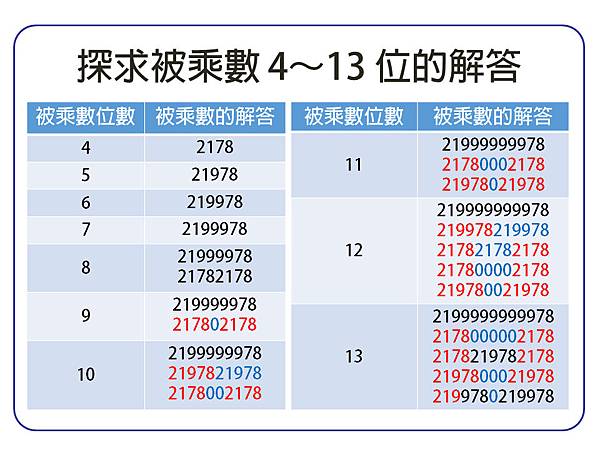
在此我們的觀察以答案的「形式」為主，在同一個被乘數位數中：

○第一種形式，是前兩位為 21、末兩位為 78，中間皆是 9。

○除了上述形式，其他答案可分成若干「段」，且每「段」的「長度」有大有小，排列呈現迴文數的性質。

※鏡子乘法解形式猜想：多位數皆由二位或四位的「原始解」「擴張」而成，就如2178的擴張方式。

 

●鏡子乘法解的數目

若將被乘數的位數以「奇」「偶」來分類，觀察它們的解答數目：

   

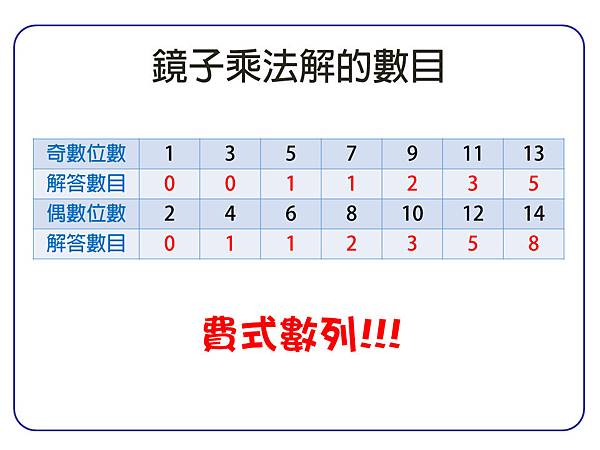
解答數目的數列，正是「費氏數列」。

 

●各進位制中的共同點

鏡子乘法解形式猜想：多位數皆由二位或四位的「原始解」「擴張」而成。

   

 

●歸納其形式變化

在 n 位中總有一種形式的解答，就是： 10(n-2)(n-1) × (n-1)＝(n-1)(n-2)01，其中 n 是該進位制的基數。我們將十～二進位的 10(n-2)(n-1) × M 的乘積列表觀察，而圖中最上方藍色的數字就是原始解：

   

 

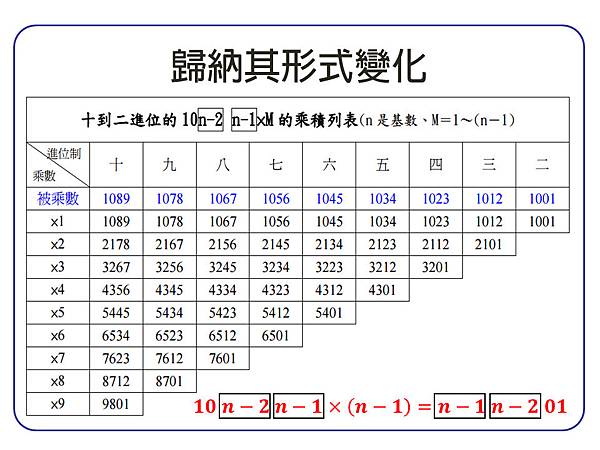
數據分析與結論

○我們給出了十～三進位(除了八進位)鏡子乘法解2～8位數之形式和其數量。

○同學們發現及證得了適用各進位制的兩個定理：林氏定理、江莊定理。

○除了 3 進位外，奇進位制的一種二位數形式解。

○推測了十～三進位的鏡子乘法解數目。

○留下鏡子乘法原始解的最終形式猜想。

 

以下是評審給的評語

   

 

【X博士評語】

一開始十進位的數字乘法中，我們可以看出這些數字的組合，都跟2178這四個數字有關係，沒想到延伸到九~二進位時，發現每個數字的組合都有屬於自己的原始解，能夠細心地尋找出這些原始解的過程，想必花費了一番苦心，而這些數字變化的奧妙，說明數學真是一門神奇的學問。

【科展解析】神奇的尺

 

上數學課時，老師給我們一支 15cm 尺，要我們畫線。這支尺沒有全部的刻度，只有 1、 4、5、11、13 ，老師問：「你們可不可以用這支尺，畫出長度為整數 1~15cm 的線？畫線要一筆畫不可用接的。」於是激起我們的興趣，就開始研究這個「刻度很少，卻能量出 1 到15跟直尺長度相同的所有整數公分長」的尺。

 

【X博士摘要說明】

1. 這支 15cm 尺所使用的刻度可不可以再少一點？


2. 尺的長度和所用的刻度個數有沒有關係？


3. 這些刻度很少的尺，可以量出最長的長度是多少？


4. 長度最長的尺，刻度要如何訂定？


5. 訂這些刻度有沒有什麼規律？

 

第 46屆 國小數學科作品

題目：神奇的尺

作者：屏東縣屏東市忠孝國民小學的同學們

 

【摘要(原文)】

本研究探討一支刻度很少而長度為整數 K公分的節約尺，這支尺可以從 1公分、2公分、3公分、…，量到 K公分，我們找出最大的 K，並且探討尺的間隔數和尺長的關係。我們發現有 N個間隔，一定會產生(N+1)*N/2 種間隔，尺長不會超過(N+1)*N/2公分。我們還找出了間隔組合總數的算法，當間隔數越多，間隔組合總數就越驚人，從幾十萬筆資料中，我們找出了 1~8個間隔的最佳解。當我們把這些間隔組合總數算法所形成的數列排在一起，發現這些數列竟然和巴斯卡三角形有關。

 

【X博士步驟說明】

●五個刻度(1、4、5、11、13)，如何畫出15公分的直線?

   

15公分尺用 5 個刻度 1、4、5、11、13 可以畫出長度為整數 1~15公分的線，用 4 個刻度不能。

 

●尺長和間隔個數有沒有關係？

如果這把尺有 N 個間隔，幾種間隔的算法就是 (N+1)*N/2 種間隔。

   

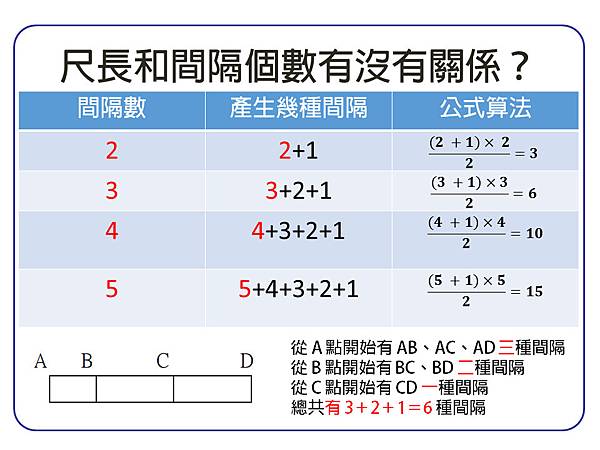
如果這把尺產生的 (N+1)*N/2 種間隔的長度沒有重覆，尺長就是 (N+1)*N/2 公分。

 

●間隔組合總數的算法

   

如果間隔數是m，尺長是 K，那麼第一個間隔組合的前面m－1 個間隔長度是 1，最後一個間隔長度就是 K－(m－1)。以下我們把間隔組合總數的算法推廣到一般情形。

3 個間隔組合總數是 1、2、3、4、5、…

4 個間隔組合總數是 1、3、6、10、15、21、28、36、45、55、66、78、…

5 個間隔組合總數是 1、4、10、20、35、56、85、120、165、220、286、…

我們把這些數列排在試算表，發現一些有趣的現象：

 

●巴斯卡三角形

   

 

數據分析與結論

這次我們做了「神奇的尺」這個題目，才發現尺只用幾個刻度，可畫出由 1公分開始到15公分尺長的線，不過還是需要一定的刻度數量，而且方法也不只一種呢！剛開始間隔少時，最佳解還好找，不過，到了五個間隔時，數量多了，算得頭都昏了，所以我們利用電腦的 EXCEL 裡的公式－COUNTIF 來找。間隔變多了，間隔組合變化也跟著變多，算間隔組合總數的算式，變得越來越長，實在看得眼花撩亂！當我們把這些間隔組合總數的數列排在一起，竟然看到了巴斯卡三角形，這尺的確是很神奇呀！

 

以下是評審給的評語

   

 

【X博士評語】

巴斯卡是十七世紀的一位法國數學家，也是歷史上第一位發明了加法計算機的人！數學中有許多秘密都隱藏在巴斯卡三角形裡!另一方面，尺是數學領域中常常用來測量的工具，如果尺上刻太多數字，會顯得特別密集，而此科展作品告訴我們可以用簡單幾個刻度就可以量出我們要的長度，如此一來，我們就不需要將每個刻度都寫出來，能有更簡單的方法。