【科展解析】數字的鏡子乘法

 

「有一個四位數 ABCD，乘以 4 後得到的答案是 DCBA，請問這個四位數是多少？」。答案為 「2178」─2178×4＝8712。然後我們想到：若這個題目的被乘數為二位到多位，會有什麼樣的答案？如果乘數換成其他正整數，又會有什麼發展？於是我們便著手研究。

 

【X博士摘要說明】

1. 出在十進位制中，符合A1×A2×A3……Am-2×Am-1×Am × N＝Am×Am-1×Am-2……A3×A2×A1的 m位數。


2. 承一，並求出解答之形式及答案數量。


3. 求出十二進位～二進位的鏡子乘法解，並探求其形式及數量。


4. 證明各進位的鏡子乘法解之一般性

 

第 47 屆 國小數學科作品

題目：數字的鏡子乘法

作者：臺北縣三峽鎮三峽國民小學的同學們

 

【摘要(原文)】

我們研究的題目是屬於「覆面算」的一種題型。探討在 n 進位制中，符合

A1×A2×A3……Am-2×Am-1×Am × N＝Am×Am-1×Am-2 ……A3×A2×A1的 m 位被乘數，其中 N＝2～(n－1)，n 為該進位制的「基數」。並歸納在所有進位制中，解答的一般性。

 

【X博士步驟說明】

●探求被乘數 4～13 位的解答(1~3無解)

   

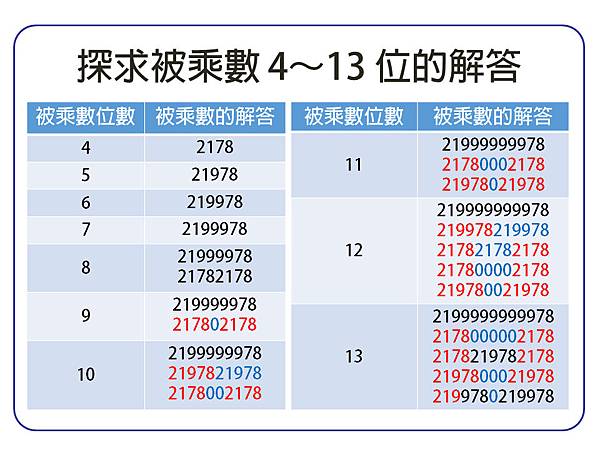
在此我們的觀察以答案的「形式」為主，在同一個被乘數位數中：

○第一種形式，是前兩位為 21、末兩位為 78，中間皆是 9。

○除了上述形式，其他答案可分成若干「段」，且每「段」的「長度」有大有小，排列呈現迴文數的性質。

※鏡子乘法解形式猜想：多位數皆由二位或四位的「原始解」「擴張」而成，就如2178的擴張方式。

 

●鏡子乘法解的數目

若將被乘數的位數以「奇」「偶」來分類，觀察它們的解答數目：

   

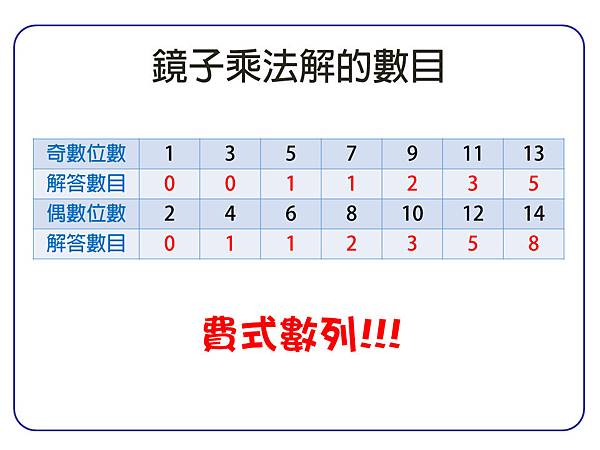
解答數目的數列，正是「費氏數列」。

 

●各進位制中的共同點

鏡子乘法解形式猜想：多位數皆由二位或四位的「原始解」「擴張」而成。

   

 

●歸納其形式變化

在 n 位中總有一種形式的解答，就是： 10(n-2)(n-1) × (n-1)＝(n-1)(n-2)01，其中 n 是該進位制的基數。我們將十～二進位的 10(n-2)(n-1) × M 的乘積列表觀察，而圖中最上方藍色的數字就是原始解：

   

 

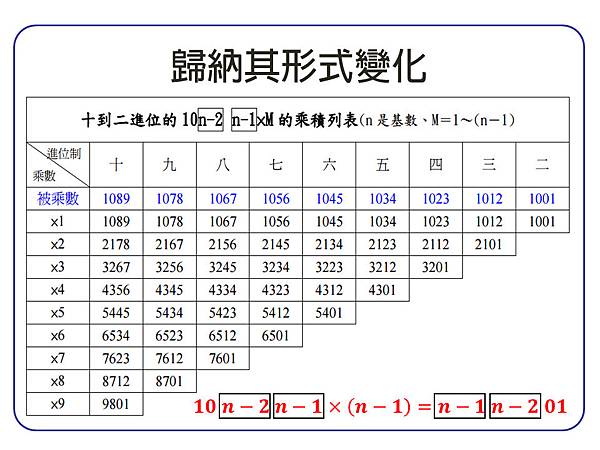
數據分析與結論

○我們給出了十～三進位(除了八進位)鏡子乘法解2～8位數之形式和其數量。

○同學們發現及證得了適用各進位制的兩個定理：林氏定理、江莊定理。

○除了 3 進位外，奇進位制的一種二位數形式解。

○推測了十～三進位的鏡子乘法解數目。

○留下鏡子乘法原始解的最終形式猜想。

 

以下是評審給的評語

   

 

【X博士評語】

一開始十進位的數字乘法中，我們可以看出這些數字的組合，都跟2178這四個數字有關係，沒想到延伸到九~二進位時，發現每個數字的組合都有屬於自己的原始解，能夠細心地尋找出這些原始解的過程，想必花費了一番苦心，而這些數字變化的奧妙，說明數學真是一門神奇的學問。